Simple Linear Regression using PyTorch

Simple linear regression is a statistical method that is used to analyze the relationship between two continuous variables:

• x - independent variable also known as explanatory or predictor.
• y - dependent variable also known as response or outcome.

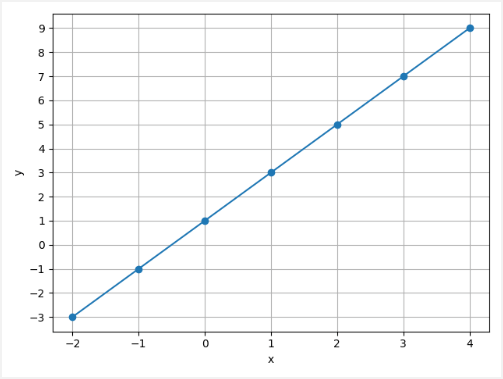
Let's say we have the following sets of numbers:

You may notice that the x value is increasing by 1, and the corresponding y value is increasing by 2. So relationship is y = 2 * x + 1.

This tutorial provides example how to create and train a model which predicts the value of y for the given value of x using PyTorch.

We define arrays of x and y values for training a model. Model contains one layer. It has one input and one output.

We choose the mean squared error (MSE) as loss function and stochastic gradient descent (SGD) as optimizer. A learning rate is 0.01.

During training, we first zero the gradients to prevent accumulation from previous steps. We perform forward pass to compute predicted y values by using x values. The loss function is used to compute the error between the predicted and true values of y. After that, we perform a backward pass and use the optimizer to update the network weights. Training is performed 400 epochs.

import torch

xs = torch.Tensor([[-2.0], [-1.0], [0.0], [1.0], [2.0], [3.0], [4.0]])
ys = torch.Tensor([[-3.0], [-1.0], [1.0], [3.0], [5.0], [7.0], [9.0]])

model = torch.nn.Sequential(
    torch.nn.Linear(1, 1)
)

loss_fn = torch.nn.MSELoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

epochs = 400
for epoch in range(epochs):
    optimizer.zero_grad()

    ys_pred = model(xs)

    loss = loss_fn(ys_pred, ys)
    loss.backward()
    optimizer.step()

x = torch.Tensor([[15.0]])
y = model(x).item()
print(y)

When the training is completed, we try to predict a value of y for a previously unknown value of x. In our case, trained model returns y equal to 31.001181 when x is 15.0. We can verify:

y = 2 * x + 1 = 2 * 15 + 1 = 31